¿Cómo forman los mosquitos esos intrigantes enjambres al atardecer? Una investigación realizada por nuestro equipo del Centro de Investigación, Innovación y Difusión en Neuromatemática (NeuroMat), de la Universidad de São Paulo (Brasil), demuestra que cada mosquito ajusta su posición en función de la proximidad de sus vecinos. Mediante simulaciones por ordenador, conseguimos formar enjambres similares a los naturales utilizando un modelo sencillo.
No obstante, no es la única teoría. Otros modelos suponen que los mosquitos se sienten atraídos por un punto central, como si estuvieran sujetos a un resorte invisible. Pero esta perspectiva quizá pueda relacionarse mejor con los casos de nubes de insectos formadas alrededor de bombillas, que no se aplican al fenómeno de aglomeración natural y que analizaremos aquí.
Otra hipótesis supone que el mosquito puede calcular la distancia que le separa del centro de la agrupación. Y la última posibilidad se basa en la densidad de mosquitos presentes en una nube, evaluando el comportamiento colectivo de estos insectos.
Así, además de cuestionar las hipótesis tradicionales, los resultados amplían nuestra comprensión de las aplicaciones biológicas de los conceptos físicos.
Cómo funciona el modelo
En el estudio de nuestro equipo, publicado en la Revista Brasileira de Física, utilizamos el concepto de vecindad de Moore, un enfoque común en los modelos informáticos que nos permite simular el espaciamiento entre los insectos en una nube.
La prueba original consistía en utilizar la información de posición de los ocho vecinos más próximos en un plano imaginario de nueve puntos. Para nuestro enfoque tridimensional, calculamos el equivalente de un cubo de 3x3x3, es decir, 26 vecinos próximos a un mosquito central.
Tal división del espacio en cuadrículas se basa en un concepto conocido como discretización. Esto no es necesario ni realista, pero basta para demostrar la idea de que los mosquitos no necesitan información a larga distancia para autoorganizarse en enjambres. Cada mosquito ajusta su posición en función de la densidad del lugar, es decir, del número de vecinos cercanos. Este planteamiento sencillo pero robusto reprodujo con precisión la formación y dispersión de las nubes, revelando patrones sorprendentes.
Transiciones de fase de segundo orden
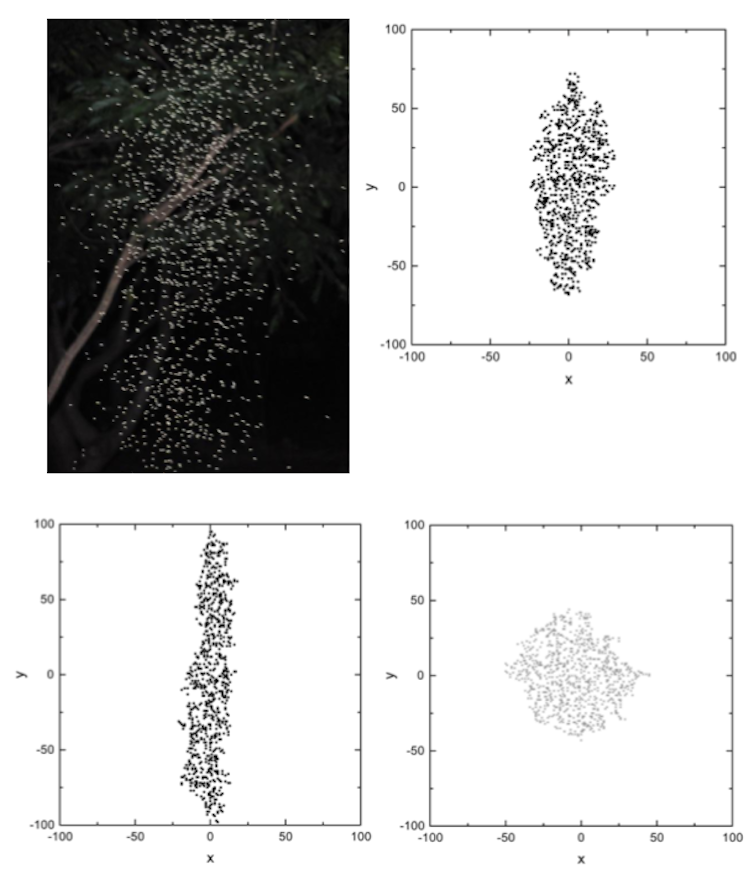
En los resultados del modelo aparecen dos fases: una con enjambres muy compactos y rígidos y otra fase con agrupaciones muy dispersas. Solo en la región de transición entre estas dos fases (la región crítica) el modelo es capaz de describir nubes de mosquitos reales.
Así pues, desde un punto de vista científico, el principal hallazgo de nuestro estudio es que los enjambres formados por mosquitos muestran un comportamiento colectivo similar a las llamadas “transiciones de fase de segundo orden”, un concepto bien establecido en física.
Este tipo de transición de segundo orden se caracteriza por una transformación continua de una sustancia provocada por un factor externo. Un ejemplo clásico es el comportamiento bien estudiado de los imanes. A medida que aumenta la temperatura, los átomos pierden progresivamente su organización magnética. Hasta que, en un punto crítico, el material deja de ser magnético.
En contraste con este comportamiento, las llamadas transiciones de primer orden implican cambios bruscos en las características físicas y químicas de determinadas sustancias objeto de estudio. El mejor y más antiguo ejemplo de ello es muy sencillo: la transición de agua líquida a vapor, acelerada por un calor intenso.
¿Y qué tiene esto que ver con el cerebro?
Las transiciones de fase y la criticidad en los sistemas biológicos son importantes temas de investigación en la física estadística actual. Este tema, que a primera vista podría parecer inconexo, llegó a NeuroMat desde la línea de investigación sobre criticidad en el cerebro (brain criticality), desarrollada por nuestra red de colaboradores.
En esta línea de investigación, hemos demostrado que las redes de neuronas pueden procesar información de forma más eficiente cuando se encuentran en un estado crítico, en el umbral de una transición de fase. En este punto, la red se vuelve más sensible a los estímulos y puede detectar señales muy débiles y muy fuertes al mismo tiempo.
Dicho mecanismo podría ayudar a explicar cómo interpreta el cerebro los olores y las imágenes, ya que se producen fenómenos similares en el sistema olfativo y la retina. Además, proponemos que la conexión eléctrica entre neuronas mejora esta capacidad, permitiéndonos percibir el mundo con mayor precisión.
Nuestro interés en esta área de investigación (de movimientos colectivos de animales, como los mosquitos), se debe a la universalidad de ideas de la física estadística que se están aplicando en biología computacional. Vale la pena recordar que el ganador del Premio Nobel de Física 2021, Giorgio Parisi, se ha dedicado intensamente a problemas de transiciones en redes neuronales. Y, recientemente, en movimientos de bandadas de estorninos. Más recientemente aún, los ganadores del Premio Nobel de Física 2024 fueron galardonados por sus ideas sobre las transiciones de fase en las redes neuronales.
Read more: Bandadas de estorninos: así se explica uno de los más bellos espectáculos de la naturaleza
Observar las transiciones de fase en fenómenos tan diferentes, desde neuronas hasta poblaciones de mosquitos, demuestra lo conectadas que están las ideas teóricas en física y biología. Es más, estos patrones también se observan en ecología, epidemiología e incluso en sociología y economía, lo que sugiere que la organización colectiva al borde de una transición de fase es un tema central en los sistemas complejos.
Aunque el estudio ha hecho avanzar la comprensión teórica del comportamiento colectivo de los mosquitos, aún quedan preguntas intrigantes: ¿cómo detectan los insectos la densidad local y coordinan sus acciones durante la transición? Estos misterios siguen fascinando y refuerzan la importancia de explorar los fenómenos cotidianos para comprender las leyes universales de la naturaleza.
Creemos que nuestro trabajo contribuye a ampliar el alcance de las ciencias matemáticas y biológicas al conectar conceptos fundamentales de la física con sistemas biológicos a diversas escalas.