Um fragmento de osso liso gravado com marcas irregulares que datam de 20.000 anos atrás – o osso Ishango – intrigou os arqueólogos até que eles notaram algo único: as gravuras, linhas como marcas de contagem, podem ter representado números primos. Da mesma forma, uma tábua de argila de 1800 AEC inscrita com números babilônicos – a tábua Plimpton 322 – descreve um sistema numérico baseado em números primos.
Como mostram o osso Ishango, a tábua Plimpton 322 e outros artefatos, os números primos fascinaram e cativaram as pessoas ao longo da História. Atualmente, os números primos e suas propriedades são estudados na Teoria dos Números, um ramo da matemática e uma área de pesquisa ativa.
Uma história dos números primos
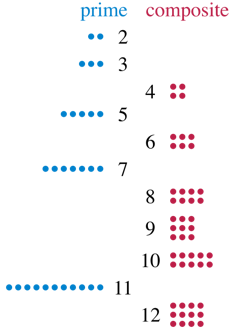
Informalmente, um número positivo maior que um é primo se esse número só puder ser organizado em uma matriz retangular com uma coluna ou uma linha. Por exemplo, 11 é um número primo, pois 11 pontos de contagem formam apenas matrizes retangulares de tamanhos 1 por 11 e 11 por 1. Por outro lado, 12 não é primo, pois você pode usar 12 pontos para formar uma matriz de 3 por 4 pontos, com várias linhas e várias colunas. Os livros didáticos de matemática definem um número primo como um número inteiro maior que um cujos únicos divisores positivos são apenas 1 e ele mesmo.
O historiador da matemática Peter S. Rudman sugere que os matemáticos gregos foram provavelmente os primeiros a entender o conceito de números primos, cerca de 500 AEC.
Por volta de 300 AEC o matemático e lógico grego Euclides provou que existem infinitos números primos. Euclides começou supondo que existe um número finito de números primos. Em seguida, ele apresentou um número primo que não estava na lista original para criar uma contradição. Como um princípio fundamental da matemática é ser logicamente consistente sem contradições, Euclides concluiu que sua suposição original deveria ser falsa. Portanto, há um número infinito de números primos.
O argumento estabeleceu a existência de um número infinito de primos, mas não foi particularmente construtivo. Euclides não tinha um método eficiente para listar todos os primos em uma lista ascendente.
Na Idade Média, os matemáticos árabes desenvolveram a teoria dos números primos dos gregos, chamados de “números hasam” nessa época. O matemático persa Kamal al-Din al-Farisi formulou o teorema fundamental da aritmética, que afirma que qualquer número inteiro positivo maior que um pode ser expresso exclusivamente como um produto de números primos.
Nessa visão, os números primos são os blocos de construção básicos para a chegar a qualquer número inteiro positivo usando a multiplicação – semelhante à combinação de átomos para formar moléculas na química.
Os números primos podem ser classificados em diferentes tipos. Em 1202, Leonardo Fibonacci apresentou em seu livro “Liber Abaci: Book of Calculation” números primos da forma (2p – 1) em que p também é primo.
Atualmente, os primos dessa forma são chamados de primos de Mersenne em homenagem ao monge francês Marin Mersenne. Muitos dos maiores primos conhecidos seguem esse formato.
Vários matemáticos antigos acreditavam que um número da forma (2p – 1) é primo sempre que p for primo. Mas em 1536, o matemático Hudalricus Regius notou que 11 é primo, mas não (211 – 1), que é igual a 2047. O número 2047 pode ser expresso como 23 vezes 89, refutando a conjectura.
Embora nem sempre seja verdade, os teóricos dos números perceberam que o atalho (2p – 1) geralmente produz números primos e oferece uma maneira sistemática de procurar por números primos grandes.
A busca por números primos grandes
O número (2p – 1) é muito maior em relação ao valor de p e oferece oportunidades para identificar primos grandes.
Quando o número (2p – 1) se torna suficientemente grande, é muito mais difícil verificar se (2p – 1) é primo, ou seja, se (2p – 1) pontos podem ser organizados somente em uma matriz retangular com uma coluna ou uma linha.
Felizmente, Édouard Lucas desenvolveu um teste de números primos em 1878, posteriormente comprovado por Derrick Henry Lehmer em 1930. O trabalho deles resultou em um algoritmo eficiente para avaliar os possíveis números primos de Mersenne. Usando esse algoritmo com cálculos manuais em papel, Lucas mostrou em 1876 que o número de 39 dígitos (2127 – 1) é igual a 170.141.183.460.469.231.731.687.303.715.884.105.727, e esse valor é primo.
Também conhecido como M127, esse número continua sendo o maior primo verificado por cálculos manuais. Ele manteve o recorde de maior número primo conhecido por 75 anos.
Pesquisadores começaram a usar computadores na década de 1950, e o ritmo de descoberta de novos primos grandes aumentou. Em 1952, Raphael M. Robinson identificou cinco novos números primos de Mersenne usando um computador Standard Western Automatic para realizar os testes de números primos de Lucas-Lehmer.
Com o aprimoramento dos computadores, a lista de números primos de Mersenne cresceu, especialmente com a chegada do supercomputador Cray em 1964. Embora haja um número infinito de números primos, os pesquisadores não têm certeza de quantos se encaixam no tipo (2p – 1) e são primos de Mersenne.
No início da década de 1980, os pesquisadores haviam acumulado dados suficientes para acreditar com segurança que existem infinitos números primos de Mersenne. Eles podiam até adivinhar a frequência com que esses números primos aparecem em média. Os matemáticos não encontraram provas até o momento, mas novos dados continuam a apoiar essas suposições.
George Woltman, um cientista da computação, fundou o Great Internet Mersenne Prime Search, ou GIMPS, em 1996. Por meio desse programa colaborativo, qualquer pessoa pode fazer download do software disponível gratuitamente no site GIMPS para pesquisar números primos de Mersenne em seus computadores pessoais. O site contém instruções específicas sobre como participar.
O GIMPS já identificou 18 números primos de Mersenne, principalmente em computadores pessoais que usam chips Intel. Em média, o programa faz uma nova descoberta a cada um ou dois anos.
O maior primo conhecido
Luke Durant, um programador aposentado, descobriu o recorde atual do maior primo conhecido, (2136.279.841 – 1), em outubro de 2024.
Referido como M136279841, esse número de 41.024.320 dígitos foi o 52º primo de Mersenne identificado e foi encontrado ao executar o GIMPS em uma rede de computação baseada em nuvem disponível publicamente.
Essa rede usava chips da Nvidia e funcionava em 17 países e 24 data centers. Esses chips avançados proporcionam uma computação mais rápida ao lidar com milhares de cálculos simultaneamente. O resultado são tempos de execução mais curtos para algoritmos, como os testes de números primos.
A Electronic Frontier Foundation é um grupo de defesa das liberdades civis que oferece prêmios em dinheiro pela identificação de números primos grandes. Ela concedeu prêmios em 2000 e 2009 para os primeiros números primos verificados de 1 milhão de dígitos e números primos de 10 milhões de dígitos.
Os próximos dois desafios dos entusiastas de números primos grandes são identificar os primeiros primos de 100 milhões de dígitos e de 1 bilhão de dígitos. Os prêmios EFF de US$ 150.000 e US$ 250.000, respectivamente, aguardam o primeiro indivíduo ou grupo bem-sucedido.
Oito dos 10 maiores números primos conhecidos são primos de Mersenne, portanto, o GIMPS e a computação em nuvem estão prontos para desempenhar um papel de destaque na busca por números primos grandes e recordes.
Os números primos grandes têm um papel vital em muitos métodos de criptografia na segurança cibernética, portanto, todos os usuários da Internet se beneficiam da busca por números primos grandes. Essas pesquisas ajudam a manter comunicações digitais e informações confidenciais seguras.